Nowatorska nieujemna metoda modelowania Bayesa służąca do przewidywania przeżycia raka przy użyciu wielowymiarowych danych omicznych Metodologia badań medycznych BMC

Strategia układania przetrwania oparta na ścieżce

Załóżmy, że dane dotyczące przeżycia są ocenzurowane N Tematy składają się z trójek {(y_I, δ_I,S_I)},l I= 1, 2, …, N. Wskazuje obserwowany czas przeżyciay_I= minuta( R_I, C_I), Gdzie R_I IC_I to odpowiednio czas zdarzenia i czas cenzury. δ_I= I ( R_I<C_I) wskazuje na wystąpienie zdarzeń. Celem jest oszacowanie funkcji przeżycia zmiennej losowej w czasie zdarzeniaY To zależy SWspółzmienne Skażdy S( y|S) = S(Y > y |S). W tym badaniu naszym celem jest przewidzenie przeżycia pacjentów chorych na raka na podstawie danych genomicznych.

Proponowana metoda układania przetrwania to dwuwarstwowa architektura uczenia się składająca się z wielu podstawowych uczniów (podmodeli) i odrębnego ucznia (metamodel). Zobacz rysunek 1, aby zapoznać się z przepływem klatek.

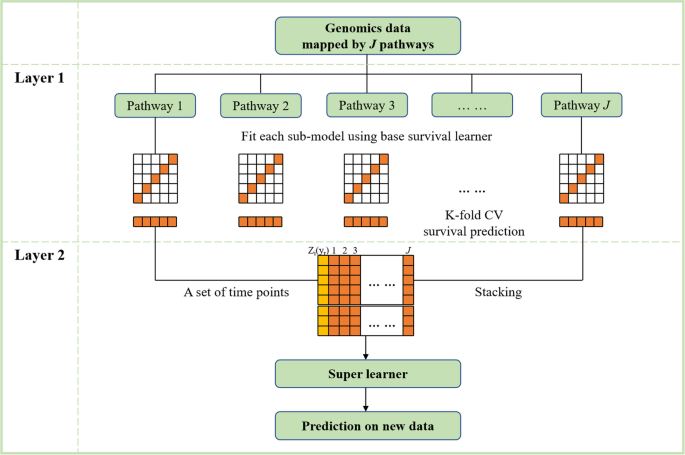
Algorytmiczny wykres przepływu proponowanego modelu układania przeżycia. CV: zweryfikowane

Najpierw przekształcamy dane genomu wCDane cząstkowe zawierające geny w każdym szlaku. Następnie w pierwszej warstwie podmodele są trenowane niezależnie dla każdego poddanych. Powstałe podmodele reprezentują moc predykcyjną trajektorii. Aby złagodzić nadmierne dopasowanie, obliczamy zweryfikowane krzyżowo predyktory przeżycia w oparciu o podmodele. W szczególności w każdym przebiegu oryginalne próbki danych są losowo dzielone KPodzbiory (fałdy) o równej (przybliżonej) wielkości. the K^y Zgięcie służy jako dane do walidacji, Piąty(K), podczas gdy pozostałe zagięcia to dane treningowe,T(-K),K= 1, 2, …, K . W danych szkoleniowych można zastosować model kar Coxa w celu dopasowania podmodelu i leżących u jego podstaw ryzykH₀^{– K}( y^–K) można oszacować metodą Breslowa. Następnie predyktor liniowy (lp^K) w danych walidacyjnych są szacowane za pomocą dopasowanego podmodelu. Szacowane prawdopodobieństwo przeżycia \({\kapelusz {S}}^k\lewo({y}^k|\boldsymbol{x}\prawo)\) WPiąty ( K ) można obliczyć za pomocąlp^K IH₀^–K( y^{– K}), że to

Gdzie \({H}^{-k}\left({y}^{-k}\right)={H}_0^{-k}\left({y}^{-k}\right)\times {e}^{l^k}\), \({H}_0^{-k}\lewo({y}^{-k}\prawo)\) Jest to skumulowane ryzyko bazowe, czyli integralna część H₀^{– K}( y^{– K}). Proces jest powtarzany dla wszystkich K fałduje, dając przewidywane prawdopodobieństwa przeżycia CV we wszystkich przypadkach. Do C Podmodele, które możemy uzyskać C Prognozy \({{\hat{S}}_j}^{CV}\left(y|\boldsymbol{x}\right)=\sum_{k=1}^K{{\hat{S}}_j}^ k\left({y}^k|\boldsymbol {x}\right),\kern0.5em j=1,2,\dots, J\). Druga warstwa wykorzystuje odrębnego ucznia, aby dopasować go do oczekiwań dotyczących przetrwania CV C Podmodele w zestawie punktów czasowych. Otrzymane współczynniki są szacunkowymi wagami \({\kapelusz{w}}_j\) DoCPodmodele. Predykcyjna funkcja przeżycia \(\kapelusz {S}\lewo(y|\boldsymbol {x}\prawo)\) Można to oszacować, łącząc predyktory CPodmodele \({\hat{S}}_j\left(y|\boldsymbol{x}\right)\) (Odnów oryginalne dane) za pomocą wag \({\kapelusz{w}}_j\).

Metoda szacowania wag \({\kapelusz{w}}_j\)

Podejście oparte na kombinacji liniowej

Zazwyczaj funkcja przeżycia ma charakter predykcyjny \(\kapelusz {S}\lewo(y|\boldsymbol {x}\prawo)\) Jest to liniowa kombinacja predyktorów C Podmodele kandydujące podane jako,

Udoskonalamy ciężary \(\kapelusz{w}\) Ograniczając zanik zespołu jelita drażliwego. Odpowiednią alternatywą powinna być inna funkcja straty, taka jak strata oparta na AUC [22]. IBS mierzy kwadrat odległości między prawdopodobieństwami a zaobserwowanymi zdarzeniami w określonym czasiey₁,…,y_S [23]które można zapisać jako,

Gdzie R( y_S) oznacza pacjentów, którzy w tym czasie nadal są zagrożeni y_S, G_I(y_S) = I( y_I> y_S). Możemy oszacować \(\kapelusz{w}\) Zmniejszając częstość występowania zespołu jelita drażliwego. Ogólnie szacunkowe wagi \({\kapelusz{w}}_j\) Ograniczone przez nieujemność dla mniejszej wariancji i lepszego przewidywania. To ograniczenie można osiągnąć stosując algorytm optymalizacji nieliniowej oparty na rozszerzonej metodzie Lagrange’a, który można zaimplementować w funkcji R. sonp [24]. Odnośnie wyboru bloków czasowych y₁,…, y_Sużywamy dziewięciu równomiernie rozmieszczonych wielkości do rozkładu obserwowanych zdarzeń, jak to nazywa Andrew Way [19].

Metoda kombinacji bayesowskiej

Oprócz rozwiązań IBS, jeśli potraktujemy predyktory przeżycia podmodelu jako współzmienne i potraktujemy przypadek zależny od czasu G_I( y_S(0) dla martwych i 1 dla żywych w każdym punkcie czasowym y_S) Jako wynik binarny oczekiwane przeżycie można wyrazić jako:

Jest to uogólniony model liniowy (GLM).H Jest to funkcja korelacji, taka jak funkcja sigmoidalna, zapewniająca, że ​​oczekiwane prawdopodobieństwo przeżycia wynosi 0-1.

Lasso nieujemne (nLasso)

Postęp wzoru (4) polega na tym, że możemy dodać Do 1 termin karny w powyższym GLM, rozszerzając w ten sposób zastosowanie stosu przetrwania, na przykład radzenie sobie z wieloma podmodelami (w scenariuszu wielowymiarowym), co jest niepraktyczne w przypadku solnp.

Wiadomo, że Lasso jest odpowiednikiem Bayesowskiego modelu hierarchicznego, w którym DE poprzedza współczynniki [25]przy współczynnikach uznawanych w tym badaniu za nieujemne,

Gdzie jest skala,S Kontroluje stopień skurczu. Mniejszy rozmiar prowadzi do silniejszego skurczu, co prowadzi do niedoszacowań Cz_Y W kierunku zera. Ciężary wyposażone w nLasso są podane przez,

Powyższe wagi można oszacować za pomocą algorytmu okresowego współczynnika współrzędnych com Pakiet w zastrzeżeniu RCz Bycie niepasywnym można łatwo wykorzystać com eksmisja.

Nieujemny kolec i lasso płytowe (nsslasso)

Rozszerzamy również nieujemny DE przed nieujemną mieszanką elewacji i płyt przed DE (rysunek uzupełniający 1),

Gdzie S_Y= (1 – γ_Y) S₀ + γ_YS₁ Nazywa się to parametrem całkowitego zakresu. γ_Y jest wskaźnikiem ( γ_Y ∈{0, 1}) po rozkładzie dwumianowym; S₀ I S₁ ( S₁ >S₀ > 0) to parametry skali odpowiednio dla wysokości i rozkładu płyty.S₁ Stosuje słabszą kompresję do silniejszych ścieżek efektów i zwykle ma ustaloną większą wartość, npS₁ = 1; chwila S₀Zapewnia silniejszą kompresję słabym ścieżkom wpływu (lub nawet kompresję do zera) i jest elastyczną mniejszą wartością wybraną z zestawu wartości kandydujących określonych wcześniej w drodze walidacji krzyżowej. Lasso kolczaste i płytowe jest zwykle bardziej elastyczne niż lasso [26]. Wagi można oszacować za pomocą algorytmu współczynnika współrzędnych EM [26] za pomocącompakiet iBahjalam package w R. Ograniczenie wag do wartości nieujemnych można również wykonać za pomocącomeksmisja.

Sztuczna sieć neuronowa

Biorąc pod uwagę, że SSN może działać jako klasyfikator i nadawać ograniczone (nieujemne) wagi danym wejściowym, możemy wykorzystać ją jako funkcję uczącą się. SSN wykorzystuje algorytm propagacji wstecznej i algorytm opadania gradientu do iteracyjnego szacowania wag.

Oceń wydajność modelu

W zasadzie model układania przeżycia jest problemem klasyfikacji binarnej dla danego okresu [21]. W tym przypadku zastosowaliśmy zależną od czasu wartość AUC i zależną od czasu skalę Briera (BS), która oblicza AUC i BS dla organizmów w grupie ryzyka w dowolnym momencie, zgodnie z zaleceniami Roberta Tibshiraniego. [21]. Zależną od czasu wartość AUC wykorzystuje się do badania zdolności modelu do rozróżniania różnych wyników w danym momencie. Zależny od czasu BS służy do pomiaru wydajności kalibracji w danym momencie: \(\textrm{BS}(y)=\frac{1}{n}\sum_{i=1}^n{\left({Z}_i(y)-\hat{S}\left(y| \boldsymbol {x}\right)\right)}^2\). Do oceny wybraliśmy trzy punkty czasowe, mianowicie 25, 50 i 75% całkowitego czasu obserwacji danych testowych.

Konkurencyjne metody statystyczne

W proponowanym przez nas modelu układania przetrwania Lasso Cox został wykorzystany do skonstruowania podmodeli opartych na ścieżkach. Aby połączyć podmodele, użyliśmy solnp (implementowanego przez funkcję Rsonp), nLasso/nsslasso (zaimplementowany w pakieciecomIBahjalam) i SSN (zaimplementowane przy użyciu biblioteki TensorFlow (2.3.0) z Pythona (3.7), a wagi można ograniczyć do wartości nieujemnych, używając kernel_constraint = Non_neg()) jako odrębnych elementów uczących. Zobacz proces syntezy SSN Dodatkowe rysunki 2 i 3. W przypadku punktów czasowych do rozkładu obserwowanych zdarzeń wykorzystaliśmy dziewięć równomiernie rozmieszczonych wielkości, a mianowicie {0, 0,125, 0,25, 0,375, 0,5, 0,625, 0,75, 0,875, 1}. Porównujemy skuteczność proponowanej przez nas metody z kilkoma istniejącymi metodami jednomodelowymi, w tym z szeroko stosowaną regresją Lasso Coxa (com.glmnet) [27] Oraz rozszerzenia zawierające struktury grupowe: Group Lasso (gsslasso) (Bahjalam) [28]grupa zagnieżdżona Lasso (grlasso), grupa zagnieżdżona cMCP i grupa zagnieżdżona płynnie wycinane odchylenie bezwzględne (grSCAD) (grpregNakładanie się) [29]. Skuteczność tych metod oceniono na podstawie danych symulowanych i rzeczywistych. Wszystkie metody pojedynczego modelu są implementowane przy użyciu parametrów domyślnych. Wszystkie analizy przeprowadzono przy użyciu oprogramowania R (4.1.3).Procesor Dell T7920 Intel Windows 10 Gold 5117 @ 2,00 GHz.