Rysunek 4 podsumowuje przewidywania HFMD przy użyciu DA-RNN. Po zebraniu i normalizacji danych cotygodniowe dane HFMD ukierunkowano za pomocą DA-RNN w celu przewidzenia tygodniowych podejrzanych przypadków HFMD na 1000 osób oraz rozróżnienia między grupami ważnych czynników meteorologicznych.
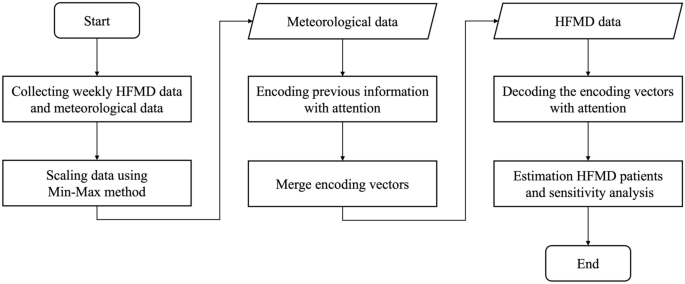
Zbieranie danych
Dane HFMD za lata 2011–2020 uzyskano na podstawie liczby podejrzanych przypadków na 1000 osób w każdym stanie, dostarczonej przez Koreańskie Centra Kontroli i Zapobiegania Chorobom.19. Jeśli chodzi o czynniki meteorologiczne, w latach 2011–2020 zebrano 15 rodzajów danych dotyczących temperatury, prędkości wiatru, opadów, długości dnia i wilgotności za pomocą Korea Meteorological Data Open Portal.20. W latach 2011–2020 za pośrednictwem AirKorea zebrano pięć rodzajów danych o zanieczyszczeniu powietrza.21.
Tabela 2 przedstawia 20 czynników meteorologicznych i opisów stosowanych do przewidywania HFMD. Czynniki pogodowe zostały podzielone na sześć kategorii: (1) Temperatura: średnia temperatura (°C), średnia maksymalna temperatura (°C), maksymalna temperatura (°C) i średnia temperatura Minimalna (°C), minimalna temperatura (°C) C). ); (2) Wiatr: średnia prędkość wiatru (m/s), maksymalna prędkość wiatru (m/s), maksymalna chwilowa prędkość wiatru (m/s); (3) Opady: średnie opady (mm), maksymalne opady (mm), maksymalne opady w ciągu 1 godziny (mm); (4) Światło słoneczne: długość dnia (godzina) i długość dnia w roku (MJ/m2); (5) Wilgotność: średnia wilgotność i minimalna wilgotność; (6) Zanieczyszczenie powietrza: SO2ku lub3NIE2i PM10. Statystyki czynników meteorologicznych przedstawiono na rys. 1B-G.
Normalizacja danych
Wstępne przetwarzanie normalizacyjne jest konieczne, gdy istnieje różnica w wielkości cech pomiędzy danymi. Normalizacja min.–maks. przekształca wszystkie cechy w zakresie od zera do jedynki22. Równanie normalizacji min-max jest następujące:
$${x}{^\prime}=\frac{x-\mathrm{min}}{max-\mathrm{min}}$$
Gdzie \(S\) Oznacza wartość każdej cechy \(S{^\główny}\) Wskazuje zmianę pomiaru. Min i max to wartości maksymalne i minimalne dla każdej funkcji.
Ocena pacjentów z podejrzeniem HFMD za pomocą DA-RNN
Tradycyjny RNN z powodzeniem wykorzystuje algorytm predykcji szeregów czasowych, który boryka się z problemem zanikających gradientów. Aby pokonać to ograniczenie, zastosowano LSTM i GRU. LSTM i GRU pokazano na rysunku S323,24. Jednak ten sam problem występuje, gdy szereg czasowy jest zwiększany. Zastosowano strukturę sieci koder-dekoder; Reprezentatywnym przykładem jest Seq2Seq25,26. Architektura ta została rozszerzona o mechanizm uwagi, który zapewnia ocenę wcześniejszych informacji, ponieważ problem pogorszenia wydajności występuje, gdy sekwencja wejściowa jest długa. Chena i in. Jako model prognozowania szeregów czasowych proponuje się DA-RNN18. Architektura ta przezwycięża niedociągnięcia modelu RNN w istniejących badaniach szeregów czasowych, wykorzystując dwa mechanizmy uwagi ze strukturami kodera i dekodera. Rysunek 5 przedstawia strukturę modelu tego badania. Mechanizm uwagi nie wykorzystuje danych wejściowych każdego punktu predykcji w tej samej proporcji, ale raczej ocenia stopień zainteresowania danymi odpowiedniego punktu predykcji i wykorzystuje je do przewidywania. Wśród różnych stopni uwagi zastosowano metodę Behdanau (sekwencja).26.
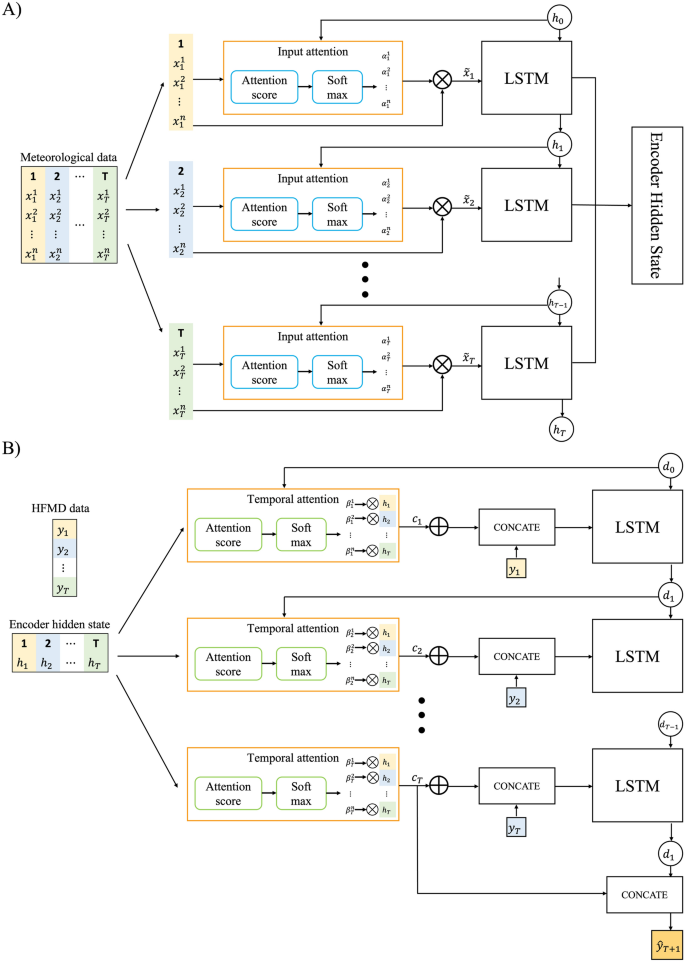
Schemat DA-RNN. (A(szyfrowanie)B) odkręcić.
W tym badaniu porównano wyniki przewidywań uzyskane przy użyciu LSTM, GRU i seq2seq, aby potwierdzić skuteczność przewidywania DA-RNN. Obliczono znaczenie czynnika pogodowego w koderze i znaczenie czasu w dekoderze. Aby potwierdzić efekt obliczenia ważności każdej struktury, porównano wyniki predykcji uzyskane za pomocą pojedynczego mechanizmu uwagi w koderze i dekoderze.
DA-RNN to algorytm oparty na koderze-dekoderze, który obejmuje mechanizm uwagi zarówno w koderze, jak i dekoderze. Tensor danych wejściowych składa się z n ciągu sterującego i n-1 ciągu docelowego w kroku czasu T, a dane wyjściowe to krok czasu T, który nazywany jest docelowym ciągiem kroków czasu T. Każdy koder przechodzi przez uwagę wejściową i LSTM kodera Struktura. Zainteresowanie wejściowe pokazane na rysunku 5 można wyrazić matematycznie w następujący sposób:
$${e}_{t}^{k} = {v}_{e}^{T}\mathrm{tanh}\left({w}_{e}\left[{h}_{t-1};{s}_{t}\right]+{v}_{e}{x}^{k}\right),$$
$${\alpha }_{t}^{k}=\frac{\mathrm{exp}\left({e}_{t}^{k}\right)}{{\sum}_{i= 1}^{n}\mathrm{exp}\left({e}_{t}^{i}\right)},$$
$$\widetilde{{x}_{t}}=\left({\alpha}_{t}^{1}{x}_{t}^{1},{\alpha}_{t}^ $$
Gdzie \({S}^{K}\) oznacza zmienną pogodową kth, \({h}_{t-1}\) oznacza ukryty stan szyfrowania, a w oznacza stan komórki szyfrowania. \({H}_{R}^{K}\) Oblicza się go metodą Bahdanau jako wynik ścierania k dla czasu t i rozkład ścierania \({\alfa }_{t}^{k}\) Obliczana jest za pomocą softmaxu i wyliczana jako wartość odsetek \(\widetilde {{x}_{t}}\) czasu t. Wyrażenie matematyczne dla kodera LSTM podano w następujący sposób:
$${f}_{t} = \sigma({w}_{f}\lewo[{h}_{t-1};\widetilde{{x}_{t}}\right]+{b}_{f})$$
$${i}_{t} = \sigma \left({w}_{i}\left[{h}_{t-1};\widetilde{{x}_{t}}\right]+ {b}_{i}\right)$$
$${x}_{t} = \sigma\lewo({w}_{x}\lewo[{h}_{t-1};\widetilde{{x}_{t}}\right]+ {b}_{x}\right) $$
$$s_{t} = f_{t} \odot s_{t – 1} i_{t} + {\text{tanh}} \odot \left({w_{s} \left[ {h_{t – 1} ;\widetilde{{x_{t} }}} \right] + b_{s} } \right)$$
$$h_{t} = o_{t} \odot{\text{tanh}} \left({s_{t} } \right),$$
Gdzie \(B\) Oznacza stronniczość, a koder LSTM ma taką samą ogólną strukturę jak LSTM. \({f}_{t}\) To brama do zapomnienia, \({On ona}\) jest bramką wejściową, \({Sekret}\) jest bramką wyjściową, \({ulica}\) jest stanem komórki, oraz \({bezpłatny}\) Jest to stan ukryty. \(\sigma\) I \(\dot\) są odpowiednio funkcją sigmoidalną i mnożeniem elementarnym.
Dekoder ma znaczenie czasowe i strukturę dekodera LSTM. Zainteresowanie czasowe wyraża się matematycznie w następujący sposób:
$${L}_{T}^{K} = {T}_{D}^{T}\mathrm{tanh}\left({W}_{D}\left[{d}_{t-1};{s}_{t-1}{^\prime}\right]+{v}_{d}{h}_{i}\right) $$
$${\beta }_{t}^{i}=\frac{\mathrm{exp}\left({l}_{t}^{i}\right)}{{\sum }_{i= 1}^{T}\mathrm{exp}\left({l}_{t}^{i}\right)}$$
$${\mathrm{c}}_{\mathrm{t}} = {\suma }_{i = 1}^{T}{\beta }_{t}^{i}{h}_{i }$$
$$ {\ widetilde {y}} _ {t-1} = {\ widehat {w}} ^ {T} \ lewo[{y}_{t-1};{c}_{t-1}\right]+\widetilde{b}.$$
Stan ukryty obliczony za pomocą kodera wykorzystano jako dane wejściowe dla uwagi czasowej. Podobnie stopień zainteresowania \({l}_{t}^{k}\) Obliczono go metodą Behdanao i rozkładem uwagi \({\beta}_{t}^{i}\) Obliczono ją za pomocą funkcji aktywacji softmax w celu uzyskania wartości odsetek czasowych \({\mathrm{c}}_{\mathrm{t}}\) W czasie t. W dekoderze LSTM obliczona wartość uwagi i poprzednia wartość docelowa \({R}_{R-1}\) Były serializowane i używane.
Wyrażenie matematyczne dla dekodera LSTM jest identyczne z wyrażeniem matematycznym dla LSTM, jak pokazano w poniższym równaniu.
$${f {^\prime}}_{t}=\sigma ({w{^\prime}}_{f} \left[{d}_{t-1};{\widetilde{y}}_{t-1}\right]+{b{^\main}}_{f} )$$
$${i{^\prime}}_{t}=\sigma \left({w{^\prime}}_{i}\left[{d}_{t-1};{\widetilde{y}}_{t-1}\right]+{b{^\main}}_{x}\right)$$
$${x{^\prime}}_{t} = \sigma\left({w{^\prime}}_{x}\left[{d}_{t-1};{\widetilde{y}}_{t-1}\right]+{b{^\main}}_{s}\right)$$
$$s_{t} ^{^\prime} = f_{t} ^{^\prime} \odot s_{t – 1{^\prime}} i{^\prime}_{t} + tanh \odot \left({w{^\prime}_{s} \left[ {d_{t – 1} ;\tilde{y}_{t – 1} } \right] + b {^\main}_{s}} \right)$$
$$d_{t} = o{^\prime}_{t} \,tanh \odot \left( {s{^\prime}_{t} } \right)$$
$$\widehat {{y}_{T}} = {v}_{y}^{T}\lewo ({w}_{y}\lewo[{d}_{T};{c}_{T}\right]+{b}_{w}\right)+{b}_{t}.$$
Model DA-RNN został wygenerowany przy użyciu Pythona 3.9.7, PyTorch 1.11, Numpy 1.21.4 i Pandas 1.3.4.
Analiza trafności prognoz
Cztery stopnie oceny — MAE, RMSE, MAPE i R2-Wyliczono w celu oceny skuteczności różnych metod przewidywania HFMD. Jeśli \({R}_{T}\) jest rzeczywistą wartością i \(\widehat {{y}_{T}}\) jest wartością przewidywaną metodami, a każdy wynik wyraża się matematycznie w następujący sposób:
$$MAE=\frac{1}{N}\sum_{i=1}^{N}|{y}_{T}^{i} -\widehat {{y}_{T}^{i} }|$$
$$RMSE= \sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left({y}_{T}^{i}-\widehat{{y}_{ T}^{i}}\right)}^{2}}$$
$$MAPE=\frac{1}{N}\sum_{i}^{N}|\frac {{y}_{T}^{i} -\widehat {{y}_{T}^{i }}}{{y}_{T}^{i}}|\razy 100\%$$
$${R}^{2}= 1-\frac{\frac{1}{N}\sum_{i}^{N}{\left({y}_{T}^{i}-\widehat {{y}_{T}^{i}}\right)}^{2}}{\frac{1}{N}\sum_{i}^{N}{\left({y}_{T ) )}^{i}-{\mu}_{y}\right)}^{2}}.$$
Ustalamy określone wskaźniki oceny dokładności (MAE, RMSE, MAPE, R2).
Analiza wrażliwości
Aby określić znaczenie sześciu grup meteorologicznych, przeprowadzono ważną procedurę grup projekcyjnych. Metryki wyniku dokładności są obliczane poprzez usuwanie każdej grupy po kolei z zespołu meteorologicznego. Im mniejsze obliczone wartości MAE, RMSE i MAPE, tym lepsza wydajność, ale im R2 jest bliższe 1, tym lepsza wydajność. Dlatego też do zapewnienia tego samego kryterium wykorzystano wartość 1-R2.
Aby ustalić ranking ważnych grup meteorologicznych, przeszliśmy przez trzy etapy. Najpierw obliczyliśmy istotną wartość wyników dokładności dla każdej grupy meteorologicznej. Dokładności całkowitego zespołu to wartości stosowane przez wszystkie zespoły meteorologiczne, a dokładności zespołu rozwijanego definiuje się jako dokładność po usunięciu jednego zespołu. Wzór na obliczenie wartości znaczącej jest następujący:
(Wartość istotna) = (całkowite wyniki dokładności grupy) – (przewidywane wyniki dokładności grupy).
Po obliczeniu tę znaczącą wartość normalizuje się do minimalnej wartości 0 i maksymalnej wartości 1. Im bliżej 1, tym większe znaczenie, a im bliższe 0, tym mniejsze znaczenie.
Po drugie, zmierzone wartości istotne wyrażono w postaci map pająków. Wiemy, że grupa o największej szerokości na tej mapie pająków jest grupą o najwyższym znaczeniu. Po trzecie, aby określić kolejność ważności, obliczyliśmy szerokość każdej grupy na mapie pająków w celu ustalenia rankingu.
Względy etyczne
W badaniu tym przeanalizowano publicznie dostępne dane HFMD i dane meteorologiczne19,2021. Publicznie dostępne dane, które nie zawierają danych osobowych, nie wymagają zgody etycznej.
„Odkrywca. Entuzjasta muzyki. Fan kawy. Specjalista od sieci. Miłośnik zombie.”
More Stories
Nowy raport WHO pokazuje, jak miasta przyczyniają się do postępu w zapobieganiu chorobom niezakaźnym i urazom
Naukowcy identyfikują „najlepszy punkt” bezpiecznej operacji po zawale serca
Badanie wykazało, że 20% dzieci chorych na zapalenie płuc nie otrzymuje antybiotyków